Por supuesto.... ¡ que no !
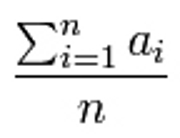
Leía yo hace un año o dos en El País que según un estudio que habían hecho unos matemáticos, el no sé cuántos por ciento, una barbaridad que no recuerdo, de los artículos publicados en las revistas científicas de mayor prestigio, contenían graves errores en el tratamiento estadístico de los datos. Naturalmente, uno no puede por menos que sonreir y pensar si no se debería hacer un "metaestudio" no vaya a ser que los estudios de cuántos artículos científicos contienen errores estadísticos contengan en un porcentaje importante a su vez errores estadísticos :-) Quizás habría que distinguir entre estudios "de primer orden", aquellos que consideren sólo estudios no referidos a estadística, y "de segundo orden", los referidos a errores estadísticos, lo cual daría lugar a una serie infinita..... Estudios sobre qué porcentaje de los estudios que calculan el porcentaje de errores estadísticos en los estudios estadísticos que...... ( así una larga serie de repeticiones, por ejemplo, para los estudios de quinto o sexto orden ^____^).
De todas formas, a mí hay uno ( un error conceptual ) que me llama la atención por lo repetido, por lo archirrepetido, por lo omnipresente. En la prensa lo veo cada poco. En literatura científica, con una persistencia intolerable.... A decir verdad no es extraño..... En una cierta Facultad de Psicología, el Plan de Estudios que yo le conocí tenía una asignatura de estadística, ni una más , ni una menos, y mis amigos que la cursaban me venían todos con el mismo comentario: jo, Sergio.... Es que la asignatura esa de Estadística que tenemos es dificilísima..... La verdad que ojeando algunos materiales suyos, a mí me parecía que su nivel no podía considerarse otra cosa que introductorio, pero aceptemos pulpo como animal marino, que lo es ( si bien también es un animal de plato, o sea que, como siempre , todo es según el color del cristal con que se mira). El que en un estudio que puede dar lugar a licenciados que se dediquen a la investigación, y que realicen estudios en que el tratamiento estadístico de datos experimentales sea esencial, a mí hacía que la asignatura se me antojara corta y poco ambiciosa, pero está claro que mi bagaje académico era muy distinto al del típico estudiante de psicología, que, con frecuencia, ni siquiera había cursado la Secundaria por vías adecuadas a las disciplinas científico-tecnológicas....
Voy al caso que ahora me ocupa: estoy leyendo una importante obra, que ha sido muy influyente , y lo sigue siendo, durante ya muchos años en su campo. A día de hoy, a mí me es importante y necesaria. Su autor describe sus investigaciones, el diseño de sus experimentos, su transcurso, sus resultados..... La metodología la encuentro excelente. Es obvio que, siendo la obra sobre un campo en principio alejado de lo más tradicionalmente considerado científico, sus preocupaciones y las técnicas que aplicó para no confundir causalidad con correlación, descubren a un académico extremadamente riguroso y conocedor del terreno que pisa.....
Y entonces...... ¡ Zack ! El tortazo. El mismo error de siempre. En un cierto punto de la obra, me encuentro con la siguiente afirmación, referida a un test al que el autor sometió a una serie de personas, cada una de las cuáles obtendría en él una puntuación entre 0 y 20 ( el autor habla en futuro porque narra sus investigaciones desde que aún era estudiante universitario y ya investigaba hasta el momento en que escribe, en secuencia cronológica; la cita no es literal porque mi texto está en inglés y lo que entrecomillaré será la mejor traducción de que soy capaz, pero aun con las deficiencias de este torpe traductor, el error lo traslado fielmente, aseguro): "Por supuesto, la mitad de los probandos obtendrán una puntuación inferior a la media y la otra mitad una puntuación superior a la media".
¡ Pues no señor ! Es el omnipresente error al que me refería.... Puede darse el caso, pero en general no tiene por qué ser así. Doy por descontado que se refiere implícitamente a la media aritmética ( cualquier otra es menos usual en un tratamiento básico y no cambiaría en todo caso la cuestión). Creo que quien tenga unos mínimos conocimientos de estadística ya lo ha visto. Para el lector que carezca de ellos pero sepa leer ( cosa que doy por supuesta si has llegado hasta aquí), pondré un sencillo y evidente contraejemplo donde podrá ver lo desafortunado de la aseveración. Con 25 probandos, que obtuvieran los siguientes resultados, 7. 8, 7, 9, 18, 8, 9, 9, 7, 8, 9 , 20, 9, 7, 19, 8, 9, 19, 8, 7, 17, 9, 20, 8 y 9. Si no me he equivocado al hacer las cuentas, ni al transcribir un pedazo de papel en que improvisé el contraejemplo, la media aritmética de esos 25 valores resulta ser 10,72. Si cuento bien, eso significa que, en este ejemplo 20 de los 25 probandos han obtenido valores inferiores a la media , mientras los otros cinco los han logrado superiores. O sea, nada de mitad y mitad. 80% y 20%.
Me gustaría ver ediciones anteriores de este libro. Es un clásico, del que no daré ni título ni autor, muy conocido en su campo, muy respetado ( con muy buenos motivos ), y se trata de la tercera edición . Sospecho que no es el tipo de error que uno introduce en la tercera edición no estando presente en las anteriores, aunque podría ser. En todo caso, uno entiende ese conocidísimo error ( "no lo llaman un clásico, a ese error, lo llaman El Quijote", recuerdo haberle oído respecto de otro en el campo del cálculo infinitesimal a un profesor, con sarcasmo .... creo que éste bien podría asumir tal nombre en el ámbito de la estadística, o, alternativamente, jugando con el título de La Divina Comedia, podría bautizársele como La Endiablada Tragedia ) en un periódico que recibe un texto y quiere publicarlo ese mismo día y las prisas explican muchas cosas.... Pero en un libro, con todos los filtros que se supone tiene que pasar, publicado por una prestigiosa editorial que lleva décadas publicando textos científicos, entre otros......
Un poco de rigor, se lo pido..... Aunque sea por San Antonio de Padua, llamado así porque nació en Lisboa :-))))
2 comentarios
Sergio -
Guti -